I’m a huge proponent of estimating in story points. (You can get a full overview of how to use story points from reading What Are Story Points.)
In all of my training and writing about story points, user stories, planning poker, and agile estimating, I’ve been quite adamant that story points are about effort. I’ve also explained that we talk about that effort in terms of how long it will take to finish because that’s 1) how we naturally think about the effort involved to do a task and 2) how we can answer questions about when a project can be delivered.
But when I say that agile story points are about effort and that effort is measured in time, it doesn’t mean teams should say, “One story point equals eight hours.” Nor ask, “One story point is how many hours?” Equating story points to a set number of hours is a bad idea. Don’t do it.
Equating hours to story points obviates the primary reason to use story points in the first place: Story points are helpful because they allow team members who perform at different speeds to communicate and estimate the amount of work collaboratively.
Story points work because they are relative units of measure, whether you are estimating with a set of cards, T-shirt sizing, or the Fibonacci series. (For more on why relative estimates are essential, read The Main Reason to Use Story Points.)
Agile Estimation Is Abstract On Purpose
By using story points, agile teams with developers who work at different speeds can agree on estimates. A senior developer might be able to knock out a certain product backlog item in 8 hours, and a more junior developer might take 16 hours to do the same work, but they can both agree that it’s a 1-point story.
With that agreement in place, they can look at another story and agree that it will take twice as much effort, so it should be worth two points. Or it’s five times as much effort, and should be five points.
Let’s look at an example. For simplicity, let’s assume the team has two members:
- Superstar
- Junior
Superstar is more experienced, skilled, and knowledgeable than Junior. This leads to Superstar being four times more productive than Junior. Any task that Junior can complete in four hours, Superstar can complete in one.
This team of 2 has an average velocity of 25 story points per sprint. This leads to them planning to complete the following product backlog items in the coming sprint.
| Images | points |
|---|---|
| A | 10 |
| B | 5 |
| C | 5 |
| D | 5 |
Because Superstar is four times more productive than Junior, Superstar will be able to complete four times as many points in the sprint. That means Superstar will complete 20 and Junior 5 of the 25 points planned in the sprint.
Junior can work on any of the five-point items and successfully complete it during the sprint. Let’s assume Junior chooses item D. That leaves Superstar with items A, B, and C as shown below.
| Items | Points | Superstar | Junior |
|---|---|---|---|
| A | 10 | X | |
| B | 5 | X | |
| C | 5 | X | |
| D | 5 | X | |
| Total | 20 | 5 |
So what do we tell someone who asks, “How many hours does it take to complete one point?”
If we assume this example is a 1-week, 40-hour sprint, there are 3 possible answers.
- Superstar worked 40 hours and delivered 20 points. Therefore, one point takes two hours of work.
- Junior worked 40 hours and delivered 5 points. Therefore 1 point takes 8 hours. Note that Junior’s number of hours per point is 4 times that of Superstar. This corresponds to the initial assumption that Superstar is 4 times as productive.
- Together, they worked 80 hours and completed 25 points. Therefore, 1 point takes 3.2 hours (80/25).
You can see from this example that there is no equivalence between points and hours. You cannot say one point equals such-and-such number of hours. For Superstar, a point is 2 hours, for Junior it’s 8 hours, and for the team it is 3.2 hours.
But if the team doesn’t listen to me, and they define a point as being equal to 3.2 hours, Junior and Superstar will not be able to agree on estimates because they produce such dramatically different results in 3.2 hours.
With story points, on the other hand, everyone can talk about and estimate the work, and the estimate will be accurate no matter which developer works on the story. In this way, story points are still about effort, but the amount of time it takes to complete each point is not fixed at the same amount for all team members.
Equating Story Points to Hours Complicates Thinking
The second problem with equating story points to a set number of hours is that team members no longer think abstractly. If someone instructs team members that one point equals eight (or any number of) hours, the benefits of estimating in an abstract but relatively meaningful unit like story points are lost.
When you try instead to convert story points to hours, you suddenly initiate an hours-to-story-points calculator in every team member’s head. When told to estimate the effort required for a story with a specific time per point in mind, the team member will mentally estimate first using the number of hours and then convert that estimate to points.
So in our first example, a senior developer who could complete a story in eight hours would call a product backlog item a one-point story (8/8=1 point). A junior developer who might take sixteen hours to do the work would call that same product backlog item a two-point story (16/8=2 points). Mathematically, they’d both be right, but they’d be miles away from each other in terms of agreeing on an estimate.
When story points are tied to a certain number of hours, story points are no longer relative. Story point estimation becomes entirely dependent on who is doing the work.
If someone in your company wants to start translating story points to hours, just stop calling the units points and use the label of hours or days instead. Calling them points when they’re really just hours introduces needless complexity (and loses one of the main benefits of points: team members with different skill levels have a common unit of measure).
The Relationship Between Story Points and Hours
So is there a relationship of agile story points to hours? Yes. Suppose for some reason you have tracked how long every one-story-point story took to develop for a given team, and stored it in a story-points-to-hours table. If you graphed that data you would have something that would look like this:
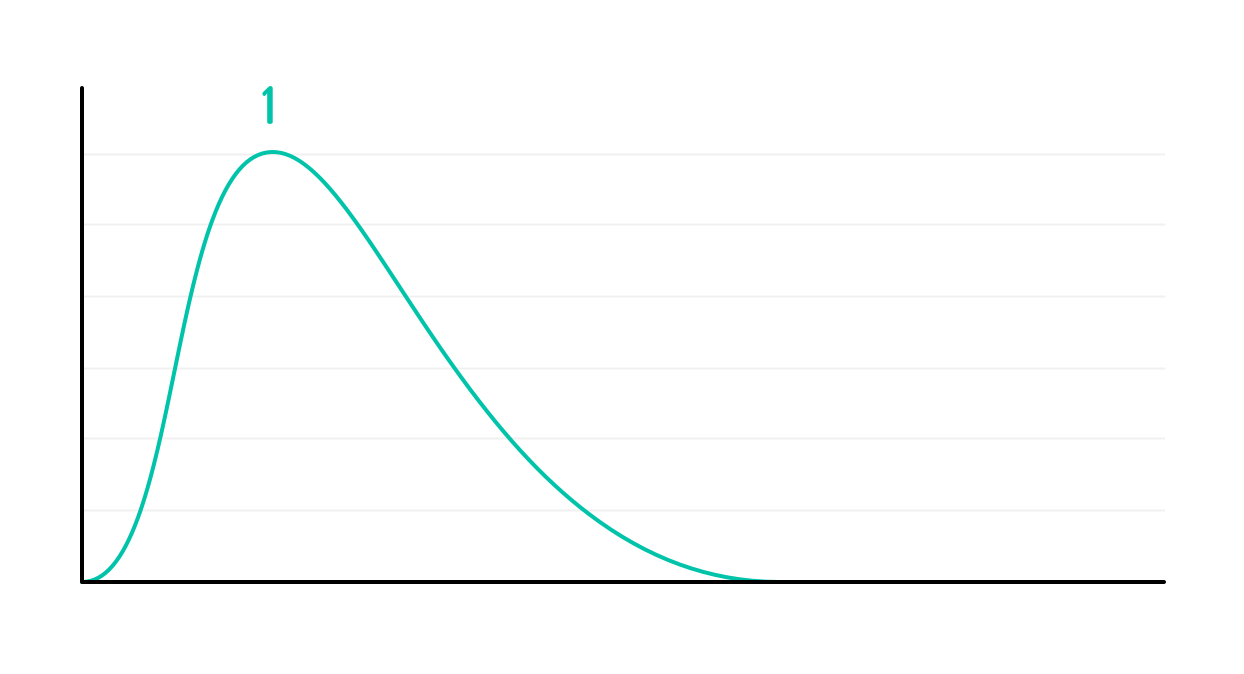
This shows that some stories took more time than others and some stories took less time, but overall the amount of time spent on your one-point stories takes on the shape shown.
Now suppose you had also tracked the amount of time spent on two-point user stories. Graphing that data as well, we would see something like this:
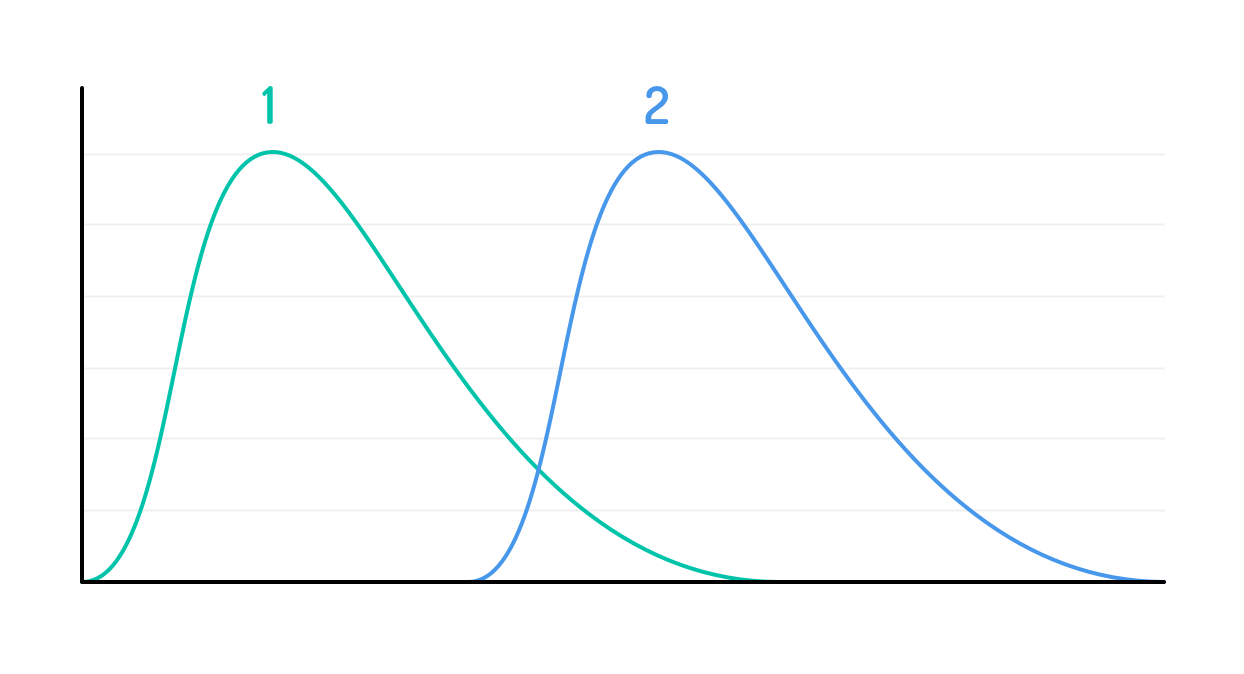Ideally the two-point stories would take twice as long as the one-point stories. That’s unlikely to be exactly the case, of course. But a team that does a good job of estimating will be sufficiently close for reliable plans to be made from their estimates based on their average team velocity.
What these two figures show us is that the relationship between points and hours is a distribution. One point equals a distribution with a mode of x, two points equals a distribution with a mode of 2x, and so on.
By the way, notice that I’ve drawn the distributions of one- and two-point stories as having overlapping tails. It is very likely that some of the most time-consuming one-point backlog items take longer than some of the shortest two-point items. After all, no team can estimate with perfect insight, especially at the story point level.
So, while the tails of the one- and two-point distributions will overlap, it would be extraordinarily unlikely that the tails of, say, the one- and thirteen-point distributions will overlap (I’m assuming here that you are using a modified fibonacci sequence for your story points, but you could use any set of numbers).
Story Points and Hours Are Not Equivalent
Some agile teams define the relationship between story points and hours as an equivalence. That is one point equals some number of hours. And by extension, two points is twice that number of hours and so on.
This is a mistake, and makes points irrelevant because they simply become a translation of hours. Mapping story points to hours makes it impossible for team members who produce their work at different rates to agree on estimates. Teams that convert Jira story points to hours through a fixed equivalence (such as one point equals eight hours) will end up with inaccurate plans.
These problems recede when teams understand that the relationship between story points and hours is a distribution. That is, one-point items take from x to y hours. And two-point backlog items take from about 2x to 2y hours.
When doing agile estimating, converting story points to hours through a simple one point equals x hours formula will result in misleading answers that are overprecise. A better way to give stakeholders a sense of how long aa story will take is to use velocity. Suppose, for example, someone wants to know how long a 5-point backlog item will take and that your team’s average velocity is 20. You can tell them that the five-point item is about one-fourth of the team’s total capacity for the sprint.
Convert Story Points to Dollars Instead
With that being said, at some point your stakeholders are still going to ask you to “translate all those crazy agile fibonacci story points to hours so I know what it means”. It's understandable. They want merely to know how to interpret the story points we tell them.
These stakeholders are accustomed to hearing how much time and money a project will take. And it’s important that teams and their leaders communicate with stakeholders in the terms those stakeholders prefer.
Fortunately, it is quite straightforward to convert an estimate of points into money. Here’s how.
- To start, gather data on how much the team has been paid over a period of time. Ideally this should be at least a few months, but you could start with as little as one sprint.
- Next, divide total team compensation by the number of story points delivered by the team in that period. This gives you a cost per point. For example, suppose a team has been paid $100,000 over some period. During the same period, the team delivered 100 story points. Dividing $100,000 by 100 gives a cost per point of $1,000.
- Multiply the cost per point by the total expected size of the project to give an estimate of the total financial cost.
You can get fancy with this calculation, if you’d like. Instead of using compensation as I did in the previous example, you might want to use fully loaded labor cost. As its name implies, this includes compensation as well as other costs such as benefits, overhead, and payroll expenses (taxes, Social Security in the U.S., etc.).
A company controller can easily (and usually immediately) provide this as a percentage. It will typically be in the range of 25–40% added to compensation.
You can get even fancier by trying to adjust for seasonality or team size changes. However, that’s usually not worth the effort: it shouldn’t significantly impact the cost per point.
Whether you choose to communicate using compensation or fully loaded labor cost, it's important to keep it simple. Everyone appreciates being communicated with in terms they understand. Clearly communicating with your stakeholders in terms of expected costs will go a long way to building trust.
Going Further
If you want to ensure you understand story points, I suggest this on-demand video course on Estimating with Story Points.
